Cylc Scheduler Internals - Part 1

This is the first post in a series of three (or maybe four later) based on diagrams I collected while debugging the Cylc scheduler. The scheduler is called by the cylc start utility.

NB: this is a post to remember things, not really expecting to give someone enough information to be able to hack the Cylc Scheduler (though you can and would have fun!).

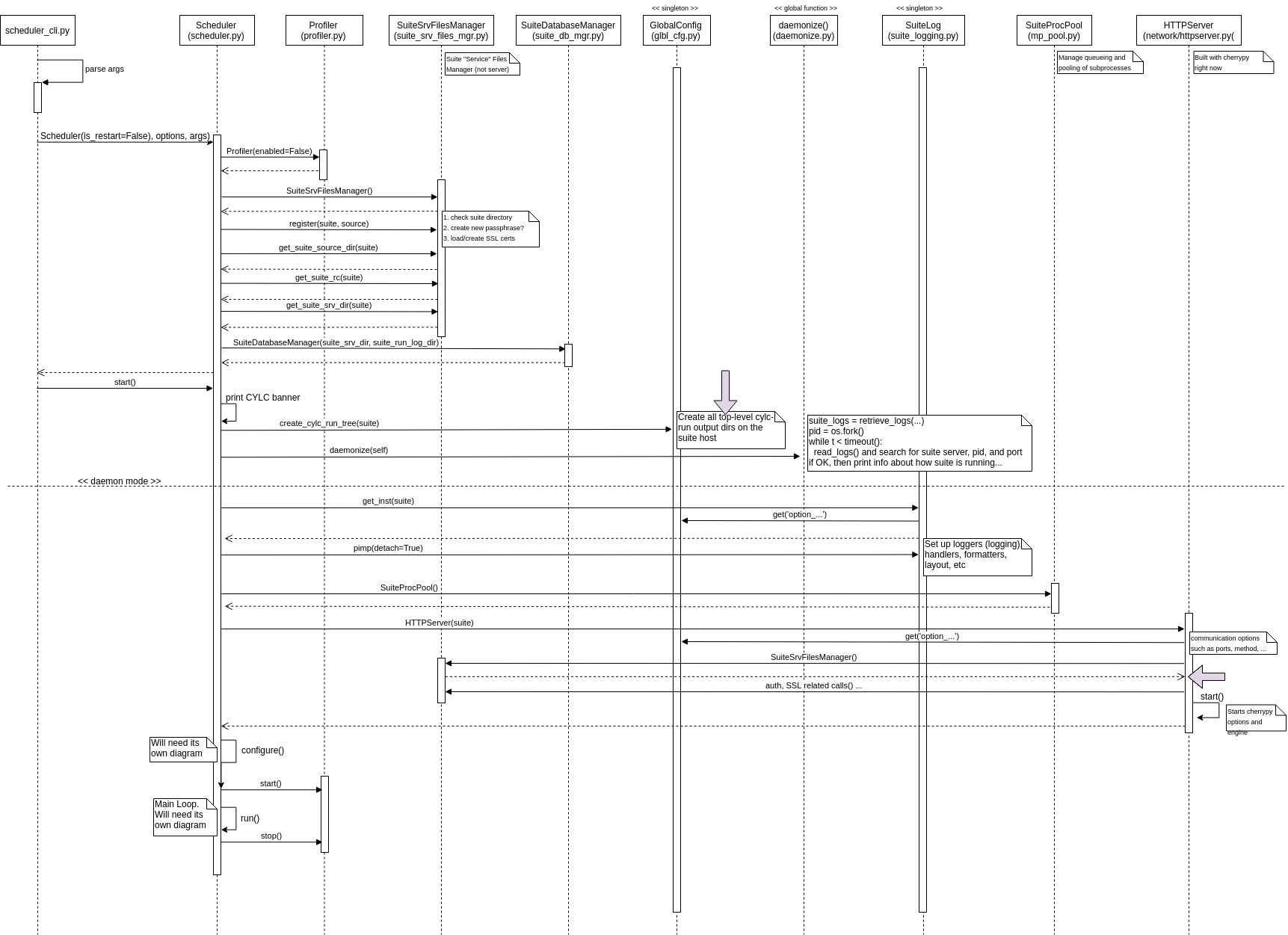
Instead of going at length on what happens (and there is quite a bit happening when you run cylc start my.suite), I will use the following diagram, followed by a few paragraphs to highlight certain parts. The code used was based on Cylc 7.7.1.

When a Cylc command like cylc start is invoked, it actually gets translated into bin/cylc-$command_name. cylc-start is a Shell file, that will simply call cylc-run. cylc-run then imports scheduler_cli… but what you need to know is that in the end scheduler_cli will create an instance of Scheduler with the right constructor arguments, and call its start method.

After that point, you are at the left-most lifeline, on the Scheduler constructor (i.e. the init method of the scheduler.py’s Scheduler class).

If you follow the method calls - which are hopefully easy to understand and follow - you will find that the constructor merely creates a few objects, prepares the suite information, and the suite database.

Then the start method kicks things off, interacting with previously created objects, but also with some singletons for logging and configuration. Oh, that Cylc banner is also printed here (in case you would like to customize it as in SpringBoot).

After that, if you are running the suite as daemon, it will be daemonized, by forking the current process, but with Python.

One important step that happens here, is the initialization of the HTTP Server. This server will be used to communicate with the Suite Server Program. It will be listening to connections with the right endpoints available only after the configure method.

Lastly, we have configure and run methods, which are two very important methods to be discussed in the next part of this series, as they are quite extensive, and deserve their own diagrams.

You can download the <a href="/assets/posts{{page.path | remove: “.md” | remove: “_posts” }}/cylc-scheduler_cli-workflow-src.png">source file for the diagram used in this post, and edit it with draw.io.

Categories: Blog

Tags: Cylc, Python, Opensource